Distribution d'échantillonnage de la moyenne
Dans cet article, nous nous intéressons aux moyennes d’échantillons. Nous devons donc débuter en décrivant la spécificité de la distribution d’échantillonnage de la moyenne. Pour ce faire, nous proposons une démonstration par le biais de R.
Le théorème central limite résume, à lui seul, les spécificités de ce type de distribution. Ce théorème stipule qu’une somme de variables aléatoires identiques et indépendantes tendra le plus souvent vers une variable aléatoire gaussienne.
Démonstration !
Nous commençons par générer une suite de 500 000 nombres aléatoires.
# Ici 500 000 nombres compris entre 0 et 100 sont générés de façon aléatoire avec remise.
s1 = runif(500000, min=0, max=100)
# Plot : On observe la forme de la distribution
h = hist(s1, freq=T, breaks=100)
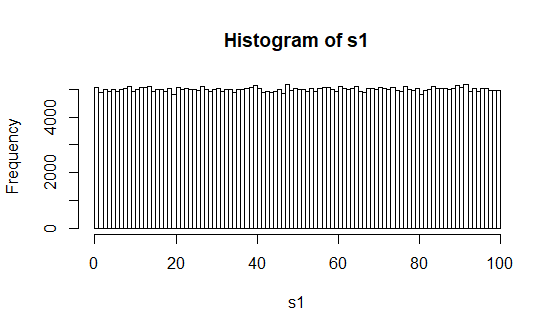
Parmi ces 500 000 nombres, nous tirons au sort plusieurs échantillons d’un effectif égal à 5 (n = 5) et nous calculons leurs moyennes. Puis nous faisons varier le nombre d’échantillons et observons les différentes distributions.
# Boucle permettant de tirer au sort des groupes de 5 nombres parmi ceux générés plus haut + calcule de leurs moyennes
count <- 0
consigne_by_sample = 5
nb_of_draw = 100
listmean = 0
repeat {tt = mean(sample(s1, consigne_by_sample))
listmean = append(listmean, tt)
count = count +1
if (count == nb_of_draw ) {
break
}
}
# Affichage des distributions
h1 = hist(listmean, freq=T, breaks=100)
xfit<-seq(min(listmean),max(listmean),length=40)
yfit<-norm(xfit,mean=mean(listmean),sd=sd(listmean))
yfit <- yfit*diff(h1$mids[1:2])*length(listmean)
lines(xfit, yfit, col= »blue », lwd=2)
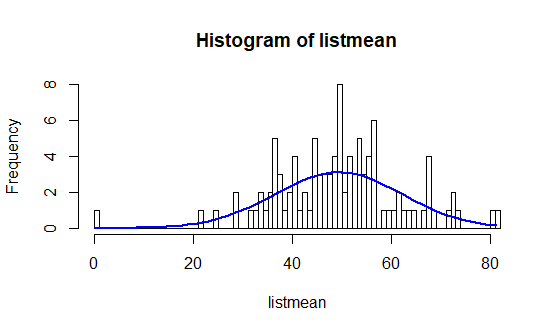
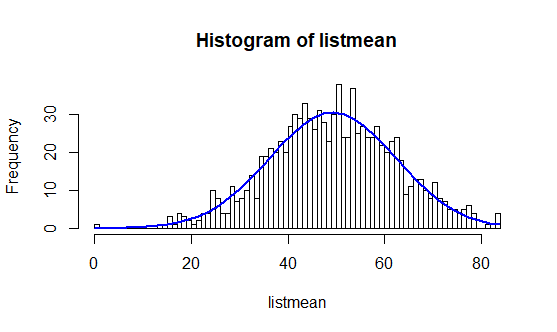
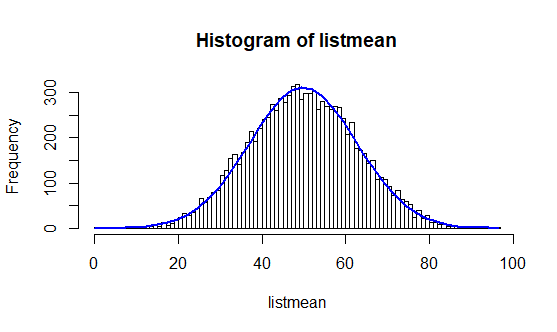
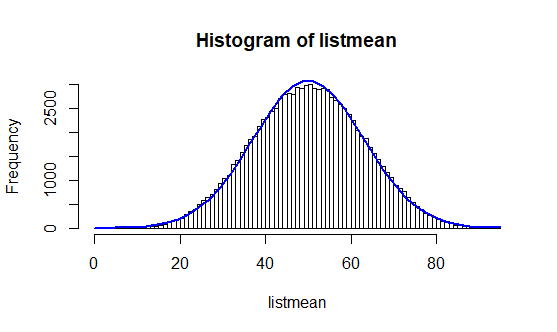
Ainsi, nous pouvons voir se réaliser la prédiction du théorème central limite au fur et à mesure des tirages. En effet, plus les tirages sont nombreux, plus la courbe a la forme d’une cloche.
Comparaison de moyennes
Il ne s’agit pas ici de comparer une observation à une distribution d’observations mais une moyenne à une distribution de moyennes (la distribution d’échantillonnage de la moyenne) (Howell, 2008).
L’utilité du t-test vient du fait que, dans une grande majorité des cas, nous ne connaissons pas la variance de la population à laquelle est appliqué le test d’hypothèse. Dans le cas contraire, il aurait été possible de calculer le score z (z = (moyenne observée – moyenne de la distribution d’échantillonnage) / erreur standard de la moyenne) afin d’exprimer (en unité : erreur standard de la moyenne) la distance entre la moyenne observée et la moyenne de la distribution d’échantillonnage, puis, de lire dans le tableau (loi normale), la probabilité d’obtenir une telle valeur. Si la variance n’est pas connue, alors nous ne calculons plus un score z mais un score t qui sera évalué par le biais d’une autre table (t). Le score t est, en fait, une transformation du score z permettant une meilleure symétrie de la distribution de la variance des distributions d’échantillonnage. Nous ne rentrerons pas davantage dans les détails.
Plusieurs applications du test de student sont possibles :
- Ce test permet de comparer une moyenne à une valeur théorique par le biais du test de student à échantillon unique (one sample t-test).
- Il permet également de comparer deux moyennes extraites de deux échantillons indépendants (test de student non apparié).
- Enfin, le test de student apparié, est utilisé pour comparer les moyennes de deux séries appariés. Par exemple, lorsque l’on mesure un temps de réaction X chez un même sujet avant et après un événement Y.
Test de student à échantillon unique (one sample t-test)
Le one-sample t-test permet de comparer une moyenne observée à une moyenne théorique.
Prenons un exemple.
Un groupe de chercheurs souhaite développer une alimentation spécifique pour les labradors. Cette race de chiens développe fréquemment de l’arthrose à l’âge adulte. Les chercheurs ont mis au point une alimentation permettant d’éviter cette pathologie. Toutefois, il se demande si cette alimentation n’engendrerait pas un surpoids à l’âge adulte. Pour tester la nouvelle alimentation, les chercheurs ont recruté 20 labradors femelles de 3 mois dont les maîtres se sont portés volontaires pour participer à l’étude. Ayant fait l’hypothèse d’un impact sur la poids, les chercheurs veulent s’assurer que les chiots recrutés sont bien représentatifs, en termes de poids, de la population générale. Ils savent qu’en moyenne le poids d’un labrador femelle de 3 mois est de 10.8 kilos.
Copier/coller les données ci-dessous dans un script R
#### Charger les packages suivants
library(tidyverse)
library(ggpubr)
library(rstatix)
#### Constitution du data set
Numero_chiots <- c(‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’, ’10’, ’11’, ’12’, ’13’, ’14’, ’15’, ’16’, ’17’, ’18’, ’19’, ’20’)
Poids <- c(9.7, 10, 8.9, 11.5, 12.1, 11.3, 9.2, 9.2, 10.1, 12.3, 9.3, 10.8, 11.2,
10.4, 9.7, 10.2, 9.9, 9.4, 10.3, 11.3)
Poids_Labrador <- data.frame(Numero_chiots, Poids)
#### Résultat du t-test
result <- Poids_Labrador %>% t_test(Poids ~ 1, mu = 10.8)
result
#### Taille d’effet
Poids_Labrador %>% cohens_d(Poids ~ 1, mu = 10.8)
Hypothèse nulle (H0) : La moyenne de poids des femelles labradors de l’échantillon ne diffère pas de la moyenne de la population générale.
Le résultat obtenu est le suivant :
| .y. | group1 | group2 | n | statistic | df | p |
| Poids | 1 | null model | 20 | -2.06 | 19 | 0.0532 |
groupe 1, groupe 2 = aux groupes comparés. Ici, le groupe 2 est nul puisque nous ne comparons pas deux moyennes mais essayons de déterminer si l’échantillon a un poids moyen significativement différent de la population générale.
n = effectif
statistic = valeur de la statistique t
df = degré de liberté = n-1
p = p-value
Taille d’effet = – 0.461 (small)
Conclusion : la p-value est inférieure à .05. Nous ne pouvons donc pas rejeter H0. Ainsi, nous pouvons conclure que le poids moyen de l’échantillon est significativement différent de celui de la population générale. Les chercheurs peuvent donc utiliser cet échantillon pour le test.
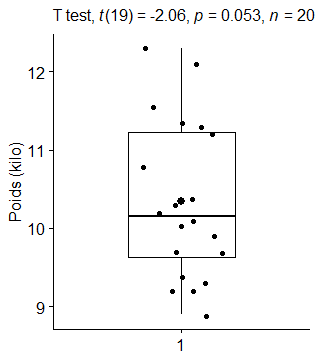
Visualisation :
Copier/coller les données ci-dessous dans un script R
#### Boxplot
bxp <- ggboxplot(Poids_Labrador$Poids, width = 1, add = c(« mean », « jitter »),
ylab = « Poids (kilo) », xlab = FALSE)
bxp + labs(subtitle = get_test_label(result, detailed = TRUE))
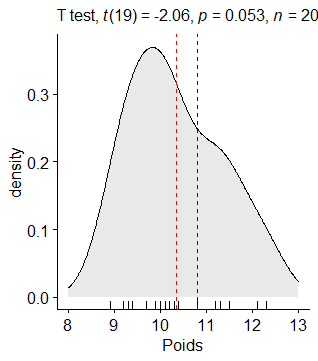
#### Diagramme de densité
ggdensity(Poids_Labrador, x = « Poids », rug = TRUE, fill = « lightgray ») +
scale_x_continuous(limits = c(8, 13)) +
stat_central_tendency(type = « mean », color = « red », linetype = « dashed ») +
geom_vline(xintercept = 10.8, color = « blue », linetype = « dashed ») +
labs(subtitle = get_test_label(result, detailed = TRUE))